Computation of Rigid Body Dynamics
import math
import matplotlib.pyplot as plt
import numpy as np
# -----========== Angular velocity ==========-----
# Calculate moments of inertia for cone from mass, height and base radius
def GetMomentsOfInertia(M, h, r):
I1 = I2 = 3 * M * (r*r + (h*h)/4) / 20
I3 = 6 * M * r*r / 20
return I1, I2, I3
def RungeKutta():
print("\n-------- Runge-Kutta --------\n")
# Find gamma terms from moments of inertia, and include the -h (step size) constant
Y1 = -stepSize * (I3 - I2) / I1
Y2 = -stepSize * (I1 - I3) / I2
Y3 = -stepSize * (I2 - I1) / I3
# Init arrays for storing W components for plotting
Wx, Wy, Wz = [Wx0], [Wy0], [Wz0]
Wmagnitude = [math.sqrt(Wx0*Wx0 + Wy0*Wy0 + Wz0*Wz0)]
# Carry out 4th order Runge-Kutta computation
for n in range(0, steps):
Kx1 = Y1 * Wy[n] * Wz[n]
Ky1 = Y2 * Wx[n] * Wz[n]
Kz1 = Y3 * Wx[n] * Wy[n]
Kx2 = Y1 * (Wy[n] + (Ky1/2)) * (Wz[n] + (Kz1/2))
Ky2 = Y2 * (Wx[n] + (Kx1/2)) * (Wz[n] + (Kz1/2))
Kz2 = Y3 * (Wx[n] + (Kx1/2)) * (Wy[n] + (Ky1/2))
Kx3 = Y1 * (Wy[n] + (Ky2/2)) * (Wz[n] + (Kz2/2))
Ky3 = Y2 * (Wx[n] + (Kx2/2)) * (Wz[n] + (Kz2/2))
Kz3 = Y3 * (Wx[n] + (Kx2/2)) * (Wy[n] + (Ky2/2))
Kx4 = Y1 * (Wy[n] + Ky3) * (Wz[n] + Kz2)
Ky4 = Y2 * (Wx[n] + Kx3) * (Wz[n] + Kz2)
Kz4 = Y3 * (Wx[n] + Kx3) * (Wy[n] + Ky2)
# Calculate and append final values
Wx.append(Wx[n] + (Kx1 + (2*Kx2) + (2*Kx3) + Kx4)/6)
Wy.append(Wy[n] + (Ky1 + (2*Ky2) + (2*Ky3) + Ky4)/6)
Wz.append(Wz[n] + (Kz1 + (2*Kz2) + (2*Kz3) + Kz4)/6)
# Calculate magnitude of W (the angular speed)
Wmag = math.sqrt(Wx[n+1]*Wx[n+1] + Wy[n+1]*Wy[n+1] + Wz[n+1]*Wz[n+1])
Wmagnitude.append(Wmag)
print("Step %s: %s, %s, %s, magnitude: %s" % (n, Wx[n+1], Wy[n+1], Wz[n+1], Wmag))
return Wx, Wy, Wz, Wmagnitude
def PlotAngularVelocity():
# Plot graph
plt.plot(timeArray, WxArray, label="ωx")
plt.plot(timeArray, WyArray, label="ωy")
plt.plot(timeArray, WzArray, label="ωz")
plt.plot(timeArray, WmagArray, label="|ω|")
plt.legend(loc="lower right")
plt.title("Angular Velocity")
plt.xlabel("time (s)")
plt.ylabel("ωi (rad/s)")
# -----========== CoM trajectory ==========-----
def SemiImplicitEuler():
print("\n-------- Semi-implicit Euler --------\n")
# Init acceleration, displacement and velocity
a = -9.8
x = [0]
v = [v0]
# Carry out computation
for n in range(0, steps):
v.append(v[n] + stepSize * a)
x.append(x[n] + stepSize * v[n+1])
print("Step %s: v: %s, x: %s" % (n, v[n+1], x[n+1]))
return x, v
def PlotCoMTrajectory():
# Plot graphs
plt.figure()
plt.plot(timeArray, v)
plt.title("Centre of Mass Vertical Velocity")
plt.xlabel("time (s)")
plt.ylabel("velocity (m/s)")
plt.figure()
plt.plot(timeArray, x)
plt.title("Centre of Mass Vertical Displacement")
plt.xlabel("time (s)")
plt.ylabel("displacement (m)")
# -----========== General motion ==========-----
def BuildRotationMatrix(a, B, Y, theta):
cosTheta = math.cos(theta)
sinTheta = math.sin(theta)
rotationMatrix = [[a * a * (1 - cosTheta) + cosTheta, a * B * (1 - cosTheta) - Y * sinTheta, a * Y * (1 - cosTheta) + B * sinTheta],
[B * a * (1 - cosTheta) + Y * sinTheta, B * B * (1 - cosTheta) + cosTheta, B * Y * (1 - cosTheta) - a * sinTheta],
[Y * a * (1 - cosTheta) - B * sinTheta, Y * B * (1 - cosTheta) + a * sinTheta, Y * Y * (1 - cosTheta) + cosTheta]]
return rotationMatrix
def SolveGeneralMotion():
print("\n-------- General Motion --------\n")
# Init variables
Px, Py, Pz = [Px0], [Py0], [Pz0]
rDash = [Px0, Py0, Pz0]
t = stepSize
for n in range(0, steps):
# Update variables for this timestep
Wmag = WmagArray[n+1]
a, B, Y = WxArray[n+1]/Wmag, WyArray[n+1]/Wmag, WzArray[n+1]/Wmag
theta = Wmag * t
# Calculate the rotation matrix for this timestep
rotationMatrix = BuildRotationMatrix(a, B, Y, theta)
# Find new rotated position using the rotation matrix
rDash = np.matmul(rotationMatrix, rDash)
# Store components of the position of the point for plotting graphs
Px.append(rDash[0])
Py.append(rDash[1])
Pz.append(x[n+1] + rDash[2]) # Center of mass only moves vertically along Z axis
print("Step %s: %s, %s, %s" % (n, Px[n+1], Py[n+1], Pz[n+1]))
return Px, Py, Pz
def PlotGeneralMotion():
# Plot graphs
plt.figure()
plt.plot(Px, Py)
plt.title("Trajectory in X-Y Plane")
plt.xlabel("x position (m)")
plt.ylabel("y position (m)")
plt.figure()
plt.plot(Px, Pz)
plt.title("Trajectory in X-Z Plane")
plt.xlabel("x position (m)")
plt.ylabel("z position (m)")
plt.figure()
plt.plot(Py, Pz)
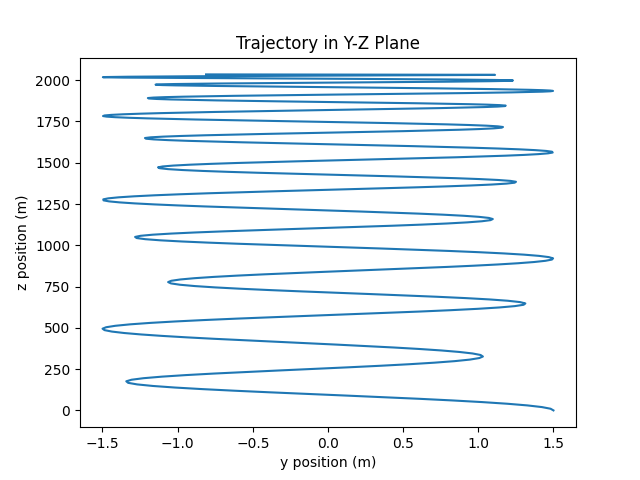
plt.title("Trajectory in Y-Z Plane")
plt.xlabel("y position (m)")
plt.ylabel("z position (m)")
# -----========== Main ==========-----
# ---- Runge-Kutta ----
# Define initial conditions, step size and number of steps
Wx0, Wy0, Wz0 = 1, 2, 3
mass = 5
radius = 2
height = 6
stepSize = 0.05
steps = 400
# Calculate moments of inertia
I1, I2, I3 = GetMomentsOfInertia(mass, height, radius)
# Do the computation
WxArray, WyArray, WzArray, WmagArray = RungeKutta()
# Populate array with values for plot's x-axis (time)
timeArray = np.arange(0, 20 + stepSize, stepSize)
# Produce plots of solutions
PlotAngularVelocity()
# ---- Semi-implicit Euler ----
# Define initial vertical velocity
v0 = 200
# Compute trajectory, where x is vertical position and v is vertical velocity
x, v = SemiImplicitEuler()
# Produce plots of solutions
PlotCoMTrajectory()
# ---- General Motion ----
# Define initial position of point P
Px0, Py0, Pz0 = 0, 0.75 * radius, 0
# Compute trajectory of point P
Px, Py, Pz = SolveGeneralMotion()
# Produce plots of solutions
PlotGeneralMotion()
# Show the graphs
plt.show()
input("\nPress Enter to exit.")
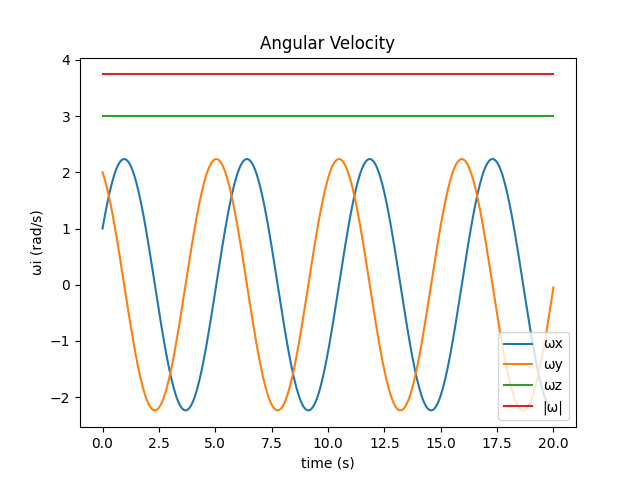
This program written in Python computes the angular velocity, centre of mass trajectory and general free motion of a rigid body in the form of a cone.
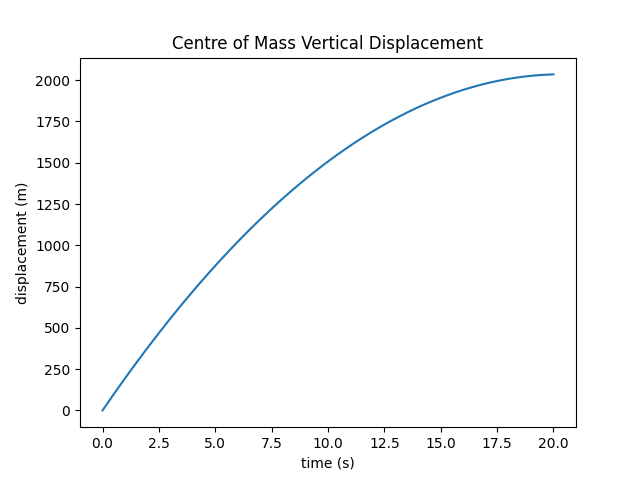
The components and magnitude of angular velocity are computed using a 4th order Runge-Kutta algorithm. The vertical velocity and displacement of the centre of mass are computed using the semi-implicit Euler method.
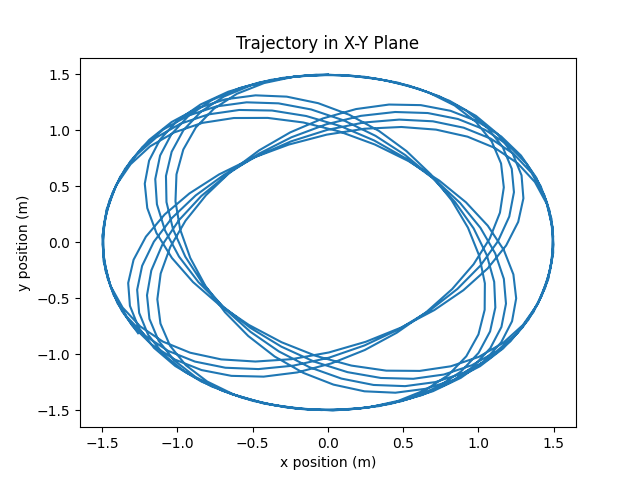
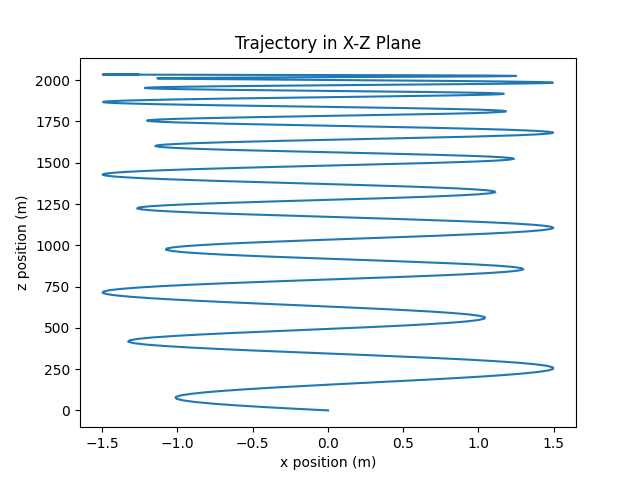
Finally the general motion is a combination of the two.
The simulation is set up for a solid circular cone of mass 5kg, radius 2m and height 6m. Initially, angular velocity ω = (1, 2, 3) rad/s.
Rotation is about an axis through the centre of mass, and the cone is given an initial velocity of (0, 0, 200) m/s and constant acceleration (0, 0, −9.8) m/s.
For general motion, the point with initial position (0, 3/4r, 0) is tracked.
Plots produced from the simulation are shown (click to open in new tab):